بدون شک اساس پردازش سیگنال دیجیتال تبدیل فوریه و پیاده سازی سریع آن یعنی fft می‌باشد. بسته های نرم افزاری طراحی شده برای محاسبات عددی اکثرا دارای توابع از پیش تعریف شده‌ای برای انجام این کار می‌باشند. یکی از این بسته های نرم افزاری پر طرفدار و کارامد در زبان برنامه نویسی پایتون SciPy می باشد. در این نوشته به معرفی نحوه محاسبه تبدیل فوریه یک سیگنال زمانی در پایتون با استفاده از امکانات کتابخانه SciPy پرداخته می شود.
بسم الله الرحمن الرحیم
کتابخانه SciPy بعنوان یکی از قدرتمندترین بسته‌های نرم افزاری موجود برای محاسبات علمی و عددی در کنار دو کتابخانه NumPy و matplotlib تقریبا تمام انتظارات شما را برآورده می‌سازد. ماژول تبدیل فوریه در این کتابخانه از scipy.fftpack قابل دسترسی می‌باشد که در این نوشته دو تابع از آن معرفی خواهد شد. تابع اول که تبدیل فوریه یک سیگنال گسسته را محاسبه می نماید fft می باشد. ابتدا بیایید سیگنال زمانی مورد نظرمان را ایجاد نماییم:
import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import fft
t = np.arange(0, 10.5, step=0.5)
time_serie = np.exp(-t)
plt.figure()
plt.stem(t, time_serie)
plt.grid(True)
plt.xticks([2, 4, 6, 8, 10],
["۲", "۴", "۶", "۸", "۱۰"])
plt.show()
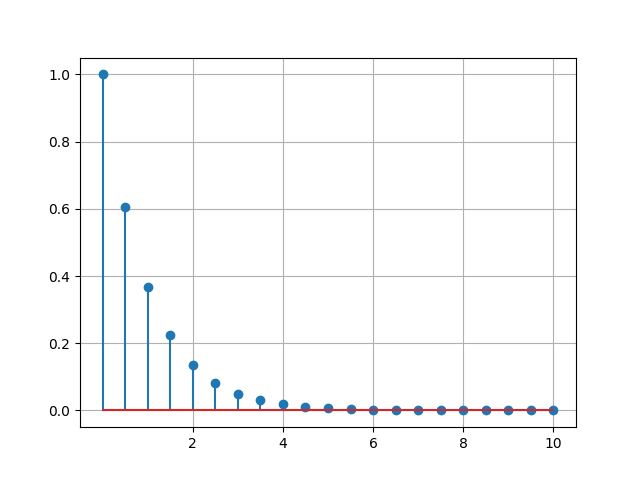
خب همانطور که می بینید سیگنال ما نمایی با ثابت زمانی ۱- می باشد. همچنین سیگنال رسم هم شده است که خروجی آن به شکل زیر می‌باشد:
حالا می رویم سراغ محاسبه تبدیل فوریه گسسته سیگنال:
fourier_trans = fft(time_serie)
plt.figure()
plt.stem(np.abs(fourier_trans))
plt.grid(True)
plt.xticks([2, 4, 6, 8, 10, 12, 14, 16, 18, 20],
["۲", "۴", "۶", "۸", "۱۰", "۱۲", "۱۴", "۱۶", "۱۸", "۲۰"])
plt.show()
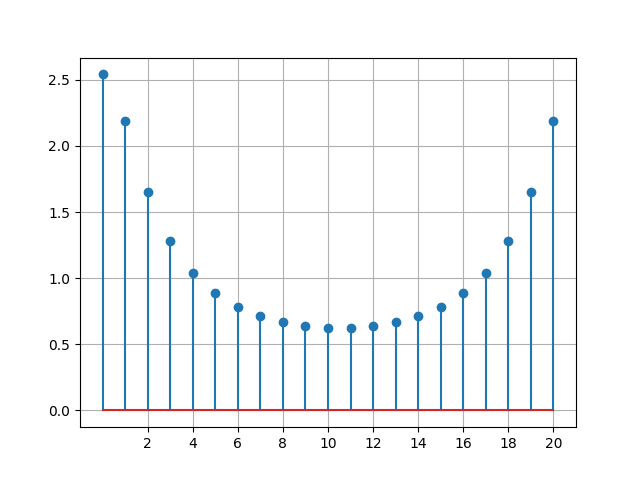
با استفاده از تابع fft از scipy.fftpack اقدام به محاسبه تبدیل فوریه و رسم اندازه آن شده است. خروجی به شکل زیر خواهد بود:
برای محاسبه عکس تبدیل فوریه نیز می توانید از تابع ifft استفاده نمایید. برای مثال اگر این تابع را با ورودی fourier_trans فراخوانی نمایید خروجی time_serie خواهد بود. (اسامی متغیرها از روی کدها گفته شده است.)