یکی از مهمترین قابلیتهای بسته های نرم افزاری برای محاسبات عددی و علمی، امکان بازنمایی اطلاعات و رسم نمودارها می باشد. کتابخانه matplotlib با ابزارهای رسم نمودارهای مختلف و متنوع دو بعدی و سه بعدی این نیاز را برای کاربران زبان برنامه نویسی پایتون فراهم آورده است. در این نوشته به انواع روشهای رسم نمودار سه بعدی در پایتون با استفاده از این کتابخانه پرداخته خواهد شد.
بسم الله الرحمن الرحیم
در کلاس pyplot از کتابخانه matplotlib توابع مختلفی برای رسم نمودارهای سه بعدی در نظر گرفته شده است که در ادامه به معرفی آنها پرداخته خواهد شد. ولی قبل از آن کتابخانه و کلاس مورد نیاز را فراخوانی کرده و یک شکل مناسب برای رسم سه بعدی آماده می نماییم. قطعه کد زیر را مشاهده نمایید:
import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() ax = fig.add_subplot(111, projection='3d')
حالا برای شروع رسم نقطه ای را در نظر می گیریم که با همان تابع متداول plot انجام می گیرد:
import matplotlib as mpl from mpl_toolkits.mplot3d import Axes3D import numpy as np import matplotlib.pyplot as plt mpl.rcParams['legend.fontsize'] = 10 fig = plt.figure() ax = fig.gca(projection='3d') theta = np.linspace(-4 * np.pi, 4 * np.pi, 100) z = np.linspace(-2, 2, 100) r = z**2 + 1 x = r * np.sin(theta) y = r * np.cos(theta) ax.plot(x, y, z, label='parametric curve') ax.legend() plt.show()
در کد بالا چهار سطر اول مربوط به فراخوانی های اولیه می باشد. سطر کد بعدی به matplotlib میفهماند که اندازه متن در نمایش برچسب نمودار رسم شده برابر ده باشد. بعد از آن با کدی که قبلا معرفی شد، شکلی مناسب برای رسم سه بعدی ساخته می شود. در ادامه محاسبات مورد نظر برای بدست آوردن مختصات سه بعدی نقاط انجام گرفته است. متغیر تتا در بازه ای از منهای چهار پی تا چهار پی با صد نمونه تعریف شده است. مختصات z در بازه منفی دو تا دو با صد نمونه تعریف گردیده و r برابر یک بعلاوه توان دوم z تعریف شده است. در ادامه با استفاده از متغیرهای r و theta دو مختصات x و y نیز محاسبه شده است. سپس با استفاده از دستور plot رسم انجام گرفته و برچسب معینی هم به نمودار داده شده است. legend فعال شده و شکل نمایش داده شده است. خروجی کد فوق به شکل زیر می باشد:
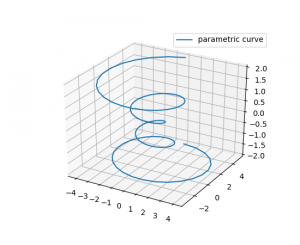همان طور که مشاهده شد در این نوع رسم نمودار ما تعدادی مختصات بطور گسسته در سه متغیر داریم که هر کدام نماینده یکی از x، y و z می باشند. هنگام رسم نمودار نقاط به هم متصل می شوند و یک خط در فضا را ایجاد می نمایند. در صورتی که اطلاعات نقاط سه بعدی در فضا به شکلی که گفته شد باشد ولی نخواهیم نقاط به شکل خطی به هم وصل شوند و بجای آن بصورت مارکرهای پراکنده در فضا باشند می توانیم از دستور scatter استفاده کنیم. به مثال زیر توجه نمایید:
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
def randrange(n, vmin, vmax):
return (vmax - vmin)*np.random.rand(n) + vmin
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
n = 100
for c, m, zlow, zhigh in [('r', 'o', -50, -25), ('b', '^', -30, -5)]:
xs = randrange(n, 23, 32)
ys = randrange(n, 0, 100)
zs = randrange(n, zlow, zhigh)
ax.scatter(xs, ys, zs, c=c, marker=m)
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
plt.show()
سه سطر اول مربوط به فراخوانی کتابخانه های مورد استفاده می باشد که مشابه مثال قبل و کد اولیه ای که معرفی شد می باشد. در ادامه تابعی تعریف شده است که دارای سه ورودی می باشد. این تابع اعداد تصادفی را به تعداد داده شده n در بازه تعیین شده vmin تا vmax ایجاد می نماید. در ادامه از این تابع برای تولید نقاطی که رسم خواهند شد، استفاده می شود. بعد از تعریف تابع، شکلی که قرار است رسم سه بعدی را بر روی آن انجام بدهیم با پروجکشن سه بعدی ایجاد شده است. در این رسم ما دو گروه داده خواهیم داشت که یکی با دایره و دیگری با مثلث در فضای سه بعدی مشخص می شوند. هر یک از این مجموعه داده ها حاوی صد مختصات سه بعدی خواهد بود. همچنین این داده ها در بازه مشخصی به شکل تصادفی ایجاد خواهند شد. همانطور که در کد هم مشهود است برای این منظور n=100 تعریف شده و حلقه for بر روی مشخصات دو مجموعه نقطه تعریف شده است. در لیستی که حلقه بر روی آن تعریف شده است، دو چند تایی وجود دارد. عنصر اول این چند تایی ها رنگی است که مارکر این مجموعه با آن مشخص خواهد شد. دومین عنصر شکل مارکر است که برای یکی دایره و برای دیگری مثلث است. عنصر سوم و چهارم نیز محدوده پایین و بالای مختصات z مربوط به هر دسته می باشد که بطور تصادفی با تابعی که ابتدا تعریف کردیم ایجاد خواهد شد. در ادامه xs، ys و zs برای scatter شدن ایجاد شده و بعد با رنگ و مارکر تعیین شده scatter می شوند. خارج از حلقه نیز برای هر یک از محورهای مختصات برچسبی تعیین شده و شکل رسم شده نمایش داده می شود. خروجی این مثال به شکل زیر می باشد:
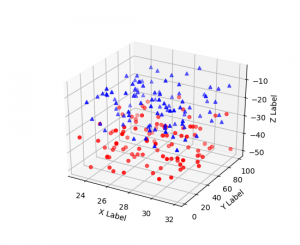نوع بعدی نمودار سه بعدی که در این نوشته معرفی خواهد شد، نمودار Wireframe یا سیمی می باشد. این نوع نمودار بر خلاف دو مورد قبلی مختصات ها را به شکل سه آرایه تک بعدی مجزا نمی گیرد. در این نوع رسم نمودار ورودی ها برای هر مختصات آرایه های دو بعدی هستند. معمولا زمانی از این نوع رسم استفاده می کنیم که بخواهیم سطحی را که در دامنه ای با مختصات x و y محدود در بازه ها تعریف شده است، رسم نماییم. مثال زیر را در نظر بگیرید:
from mpl_toolkits.mplot3d import axes3d import matplotlib.pyplot as plt X, Y, Z = axes3d.get_test_data(0.05) fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10) plt.show()
در این مثال بعد از فراخوانی کتابخانه های مورد استفاده، از داده های تست استاندارد خود matplotlib استفاده شده است. برای درک بهتر نوع پارامترهای ورودی تابع plot_wireframe حتما shape مختصاتهای X، Y و Z را مشاهده نمایید. در ادامه نیز شکل ایجاد شده و رسم انجام گرفته و خروجی نمایش داده شده است. خروجی این مثال به شکل زیر می باشد:
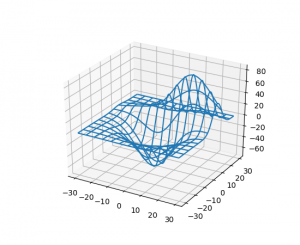تابع دیگری که برای رسم صفحه سه بعدی به کار می رود، plot_surface می باشد. ورودی های اساسی این تابع مشابه plot_wireframe است و مستقیما می توانیم در کد بالا به جای فراخوانی رسم نمودار سیمی از plot_surface استفاده نماییم. به قطعه کد زیر توجه نمایید:
from mpl_toolkits.mplot3d import axes3d import matplotlib.pyplot as plt X, Y, Z = axes3d.get_test_data(0.05) fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10) plt.show() fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.plot_surface(X, Y, Z) plt.show()
خروجی plot_surface به شکل زیر خواهد بود:
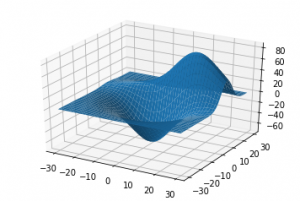در قسمت دوم این نوشته با مثالهای کاربردی تر روش های توضیح داده شده را بیشتر مورد بررسی قرار خواهیم داد و علاوه بر این روشها، متدهای دیگر رسم نمودار سه بعدی در پایتون را معرفی خواهیم کرد.