قسمت اعظمی از محبوبیت کسب شده توسط زبان برنامه نویسی پایتون علاوه بر ساختار ویژه آن، مربوط به بسته های نرم افزاری و کتابخانه هایی است که برای پشتیبانی از موضوعات مختلف در آن ارائه شده است. در این نوشته به معرفی کتابخانه منطق فازی پرداخته شده است. منطق فازی یکی از مباحثی است که مورد توجه محققین و دانشمندان می باشد و در مجامع علمی جایگاهی ویژه پیدا کرده است.
بسم الله الرحمن الرحیم
فرض بر این است که شما با منطق فازی آشنایی دارید پس می توانیم برویم سراغ کتابخانه scikit-fuzzy. ابتدا برای نصب کتابخانه فازی با استفاده از pip از دستور زیر استفاده می نماییم. اگر هر دو ویرایش پایتون ۲ و پایتون ۳ را داشته باشید و بخواهید کتابخانه را برای پایتون ۳ نصب کنید بجای pip از pip3 استفاده نمایید.
pip install -U scikit-fuzzy
خب حالا که کتابخانه نصب شده است برویم سراغ استفاده از پایهای ترین انتظارات از یک کتابخانه فازی. برای اینکه کارهایی که انجام می دهیم خیلی هم فضایی نباشد یک هدف را مشخص می نماییم. فرض کنید می خواهیم یک الگوریتم بهبود یافته مشخص کننده لبه در تصاویر بسازیم (البته عملا این کد منجر به الگوریتم مشخص کننده لبه ارتقا یافته نمیشه چون اولا برای کم کردن بار کاری، فضای متغیرهای ورودی با تعداد کمی مجموعه فازی پوشش داده شده و دوما قوانین فازی همینطوری مشخص شده اند و تنظیمی روی آنها انجام نشده است). برای انجام اینکار از یک سیستم استنتاج فازی استفاده می کنیم که دارای دو ورودی می باشد، یکی گرادیان تصویر grayscale و دومی گرادیان اشباع (saturation). قبل از رسیدن به مرحله استفاده از کتابخانه فازی ورودی های مورد نیاز را آماده می کنیم. قطعه کد زیر را مشاهده نمایید:
import numpy as np
import skfuzzy.control as ctrl
import matplotlib.pyplot as plt
from skimage import io
from skimage.color import rgb2hsv
from skimage.morphology import disk
from skimage.filters.rank import gradient, median
from skimage.color import rgb2gray
from mpl_toolkits.mplot3d import Axes3D
# %%
image_rgb = io.imread("benchmark_4.jpg")[:,:,:3]
plt.figure()
plt.imshow(image_rgb)
plt.show()
image_gray = rgb2gray(image_rgb)
image_median = median(image_gray, disk(3))
median_grad = gradient(image_median, disk(1))
median_grad = median_grad / np.max(median_grad)
image_hsv = rgb2hsv(image_rgb)
image_sat = image_hsv[:, :, 1]
sat_med = median(image_sat, disk(3))
sat_med_grad = gradient(sat_med, disk(1))
sat_med_grad = sat_med_grad / np.max(sat_med_grad)
کارهایی که در قطعه کد بالا انجام می گیرد به این شرح است که کتابخانه ها و توابع مورد نیاز فراخوانی می گردند و بعد از آن عکس از فایل مورد نظر خوانده شده و ویرایش rgb آن نمایش داده می شود. بعد از آن با تابع rgb2gray تصویر grayscale بدست می آید. برای اینکه تغییرات نامطلوب تصویر را تعدیل نماییم از فیلتر مدیان استفاده می کنیم و سپس به خروجی آن فیلتر گرادیان را اعمال می کنیم. برای اینکه کار با داده ها آسان شود با تقسیم بر ماکزیمم مقدار خروجی را نرمالایز می نماییم. در ادامه تصویر rgb را به مختصات رنگی hsv انتقال می دهیم و مشخصه اشباع آن را جدا کرده و فیلتر مدیان و گرادیان را اعمال می نماییم. با نرمالایز کردن این مشخصه دو ورودی سیستم استنتاج فازی ما آمده می شود. تصویر ورودی ما به این شکل می باشد:
لازم به ذکر است برای فیلتر های گرادیان و مدیان و دیگر کارهای انجام شده روی تصویر از کتابخانه scikit-image ستفاده شده است که با pip بصورت زیر قابل نصب می باشد:
pip install -U scikit-image
حالا نوبت به طراحی سیستم استنتاج فازی می رسد. برای اینکار ابتدا برداری را که مشخص کننده فضای کاری گسسته متغیرهای فازی می باشد، ایجاد می نماییم:
universe = np.linspace(0, 1, 10)
بعد از آن بایستی متغیرهای ورودی سیستم فازی (antacedent) را تعریف نماییم:
Gray = ctrl.Antecedent(universe, 'Gray') Saturation = ctrl.Antecedent(universe, 'Saturation')
دقت کنید که کلاس ctrl همان control کتابخانه scikit-fuzzy می باشد که یک کنترل کننده فازی برای ما ایجاد می کند. همچنین باید متغیرهای خروجی سیستم فازی را تعریف نماییم که در اینجا فقط یکی است:
Sketch = ctrl.Consequent(universe, 'Sketch')
بعد از این کار نوبت به مشخص کردن مجموعه های فازی که دامنه تعریف متغیرهای ورودی و متغیر خروجی سیستم فازی مورد نظر ما را پوشش می دهد، می رسد. ما این کار را بطور خودکار انجام می دهیم و بر عهده کتابخانه می گذاریم. کتابخانه بطور متقارن و مشابه مجموعه های فازی را ایجاد می نماید:
names = ['low', 'medium', 'high'] Gray.automf(names=names) Saturation.automf(names=names) Sketch.automf(names=names)
همانطور که می بینید ورودی ها و خروجی هر کدام با سه مجموعه low، medium و high مشخص شده است. مهمترین قسمت یک سیستم استنتاج فازی قوانین اگر آنگاه فازی می باشد. با قطعه کد زیر این قوانین اگر آنگاه تعریف می گردد. چون با مشاهده کد همه چیز دستتان می آید، توضیح اضافه نمی دهم ولی اگر سوالی داشتید کامنت بگذارید:
rule1 = ctrl.Rule(antecedent=Gray['low'] & Saturation['low'], consequent=Sketch['low']) rule2 = ctrl.Rule(antecedent=Gray['low'] & Saturation['medium'], consequent=Sketch['low']) rule3 = ctrl.Rule(antecedent=Gray['low'] & Saturation['high'], consequent=Sketch['medium']) rule4 = ctrl.Rule(antecedent=Gray['medium'] & Saturation['low'], consequent=Sketch['low']) rule5 = ctrl.Rule(antecedent=Gray['medium'] & Saturation['medium'], consequent=Sketch['medium']) rule6 = ctrl.Rule(antecedent=Gray['medium'] & Saturation['high'], consequent=Sketch['high']) rule7 = ctrl.Rule(antecedent=Gray['high'] & Saturation['low'], consequent=Sketch['medium']) rule8 = ctrl.Rule(antecedent=Gray['high'] & Saturation['medium'], consequent=Sketch['high']) rule9 = ctrl.Rule(antecedent=Gray['high'] & Saturation['high'], consequent=Sketch['high'])
با استفاده از این قوانین سیستم کنترلی به شکل زیر تعریف می گردد:
system = ctrl.ControlSystem(rules=[rule1, rule2, rule3, rule4, rule5, rule6, rule7, rule8, rule9])
حالا یک شبیه ساز برای سیستم درست می کنیم که با استفاده از آن بتوانیم ورودی های دلخواه را به سیستم داده و خروجی متناظر سیستم فازی را محاسبه نماییم:
sim = ctrl.ControlSystemSimulation(system)
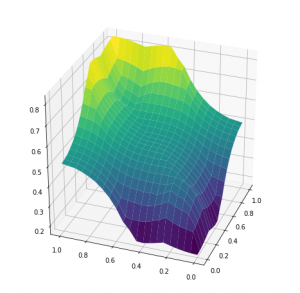
یک نمودار رایج که در سیستم های کنترلی رسم می شود، صفحه کنترلی بر اساس دو ورودی سیستم می باشد. برای رسم این نمودار برای مثال ما از قطعه کد زیر استفاده می نماییم:
upsampled = np.linspace(0, 1, 21)
x, y = np.meshgrid(upsampled, upsampled)
z = np.zeros_like(x)
for i in range(21):
for j in range(21):
sim.input['Gray'] = x[i, j]
sim.input['Saturation'] = y[i, j]
sim.compute()
z[i, j] = sim.output['Sketch']
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111, projection='3d')
surf = ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap='viridis', linewidth=0.4, antialiased=True)
ax.view_init(30, 200)
همان طور که می بینید در این کد ابتدا یک فضای دو بعدی با دامنه بین صفر و یک و تعداد نمونه ۲۱ تایی در هر بعد ایجاد شده است. سپس با دو حلقه تو در تو مقادیر از فضای دو بعدی به شبیه ساز ورودی داده شده و خروجی در z جاگذاری گردیده است. نحوه ورودی دادن و محاسبه و خروجی گرفتن از چهار سطر زیر از کد بالا کاملا واضح است:
sim.input['Gray'] = x[i, j] sim.input['Saturation'] = y[i, j] sim.compute() z[i, j] = sim.output['Sketch']
صفحه کنترلی برای مثال ما به این شکل خواهد بود:
 حال قسمت آخر کار رسیده است یعنی ورودی دادن عکس به سیستم و رسم خروجی آن. قطعه کد زیر را ببینید:
حال قسمت آخر کار رسیده است یعنی ورودی دادن عکس به سیستم و رسم خروجی آن. قطعه کد زیر را ببینید:
output_image = np.zeros(shape=np.shape(image_gray))
for i in range(np.shape(image_gray)[0]):
for j in range(np.shape(image_gray)[1]):
sim.input['Gray'] = median_grad[i, j]
sim.input['Saturation'] = sat_med_grad[i, j]
sim.compute()
output_image[i, j] = sim.output['Sketch']
plt.figure()
plt.imshow(output_image < 0.25, cmap="gray", interpolation="nearest")
plt.show()
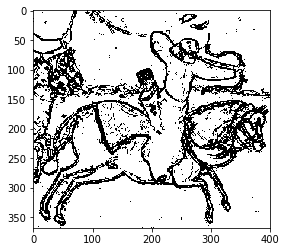
همانطور که مشاهده می شود آرایه دو بعدی هم شکل با image_gray با مقادیر صفر ایجاد شده است تا تصویر خروجی سیستم در آن ذخیره شود. با دو حلقه تو در تو دو مشخصه تمام نقاط تصویر را بعنوان ورودی داده و خروجی را حساب می کنیم و در output_image نگه می داریم. بعد از اتمام کار حلقه خروجی نمایش داده می شود که بصورت زیر است. پیشنهاد می کنم داخل تابع imshow، ترشولد را که برابر ۰٫۲۵ در نظر گرفته شده است تغییر دهید و نتایج را ببینید.
 امیدوارم از این مطلب آموزشی نهایت استفاده را برده باشید. برای خرید کدهای مثال این آموزش به شکل مجتمع می توانید به آدرس زیر مراجعه نمایید:
امیدوارم از این مطلب آموزشی نهایت استفاده را برده باشید. برای خرید کدهای مثال این آموزش به شکل مجتمع می توانید به آدرس زیر مراجعه نمایید:


بسیار عالی و مفید بود برای من.