الگوریتمهای پیمایش گراف برای مشاهده تمام رأسهای یک گراف یا جستجوی آن مورد استفاده قرار میگیرند. بسیاری از مسائل عملی میتواند در قالب یک مسئله پیمایش گراف تعریف گردد. یکی از مشهورترین الگوریتمهای پیمایش گراف جستجوی اول عمق میباشد. شروع به کار این الگوریتم از رأسی است که به عنوان ریشه گراف در نظر گرفته شده است. سپس حرکت بهسوی رأسهای مجاوره مشاهده نشده در عمق خواهد بود. بعبارتی وقتی به اولین رأس مجاور ریشه رسیدیم، نه به سراغ رأسهای مجاورِ دیگرِ ریشه، بلکه به سراغ رأسهای مجاور رأس مشاهده شده میرویم و این فرآیند تکرار میگردد تا در جهت عمق دیگر رأس مشاهده نشدهای باقی نمانده باشد. در این صورت با برگشت به سطح پیشین به پیمایش رأس مجاور دیگر به همین منوال میپردازیم.
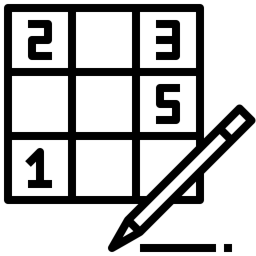
در این محصول به ارائه پیادهسازی پایتون جستجوی اول عمق برای حل سودوکو اقدام شده است. نمونه کد زیر نحوه استفاده از کلاس حل کننده سودوکوی ارائه شده را نشان میدهید:
board = [["5", ".", ".", ".", ".", ".", ".", ".", "."],
["۲", "۴", ".", "۱", ".", ".", ".", ".", "."],
[".", "۲", ".", ".", ".", ".", ".", ".", "."],
[".", ".", "۳", ".", ".", ".", ".", ".", "."],
[".", ".", ".", ".", "۴", ".", ".", ".", "."],
[".", ".", ".", ".", ".", ".", ".", ".", "۹"],
[".", ".", ".", ".", ".", ".", "۷", ".", "."],
[".", ".", ".", ".", ".", ".", ".", "۸", "."],
[".", ".", ".", ".", ".", "۶", ".", ".", "."]]
sudoku = Sudoku(board, 9, 9)
print(sudoku.solve())
print(sudoku)
محتویات بسته:
- فایل توضیح سطر به سطر کدها (ده صفحه)
- فایل پایتون کلاس حل کننده سودوکو
امیدوارم از خرید این بسته نهایت رضایت را داشته باشید. با ما در تماس باشید:
contact [at] projelecom.ir